Η κβαντική φυσική είναι ένα συναρπαστικό αλλά περίπλοκο θέμα που πρέπει να καταλάβει, και ένα από τα πράγματα που ξεχωρίζει κάθε φοιτητής φυσικής είναι η έννοια της εμπλοκής. (Στην πραγματικότητα, τα σωματίδια βρίσκονται σε πολλαπλές καταστάσεις - για παράδειγμα, περιστρέφονται σε πολλαπλές κατευθύνσεις - και μπορούν να θεωρηθούν ότι βρίσκονται σε μια κατάσταση ή στην άλλη όταν μετριούνται.)
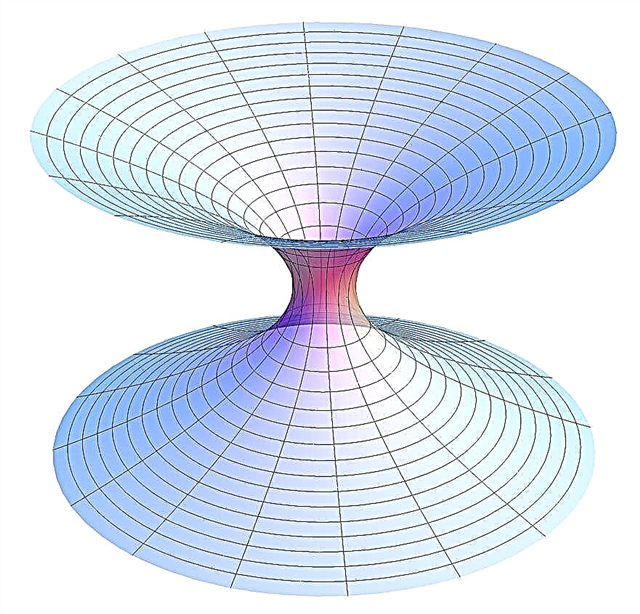
Η «τρομακτική δράση σε απόσταση» είναι ο τρόπος με τον οποίο ο Άλμπερτ Αϊνστάιν αναφέρεται σε αυτό. Εδώ είναι το νέο κομμάτι για αυτό: ο Julian Sonner, ανώτερος μεταδιδακτορικός ερευνητής στο Ινστιτούτο Τεχνολογίας της Μασαχουσέτης, οδήγησε έρευνα που δείχνει ότι όταν δημιουργούνται δύο από αυτά τα κουάρκ, η θεωρία χορδών δημιουργεί μια σκουληκότρυπα που συνδέει τα κουάρκ.
Σύμφωνα με το MIT, αυτό θα μπορούσε να βοηθήσει τους ερευνητές να κατανοήσουν καλύτερα τη σχέση μεταξύ της βαρύτητας (που λαμβάνει χώρα σε μεγάλη κλίμακα) με την κβαντική μηχανική (η οποία λαμβάνει χώρα σε πολύ μικρή κλίμακα). Όπως το θέτει ο MIT, μέχρι τώρα ήταν πολύ δύσκολο για τους φυσικούς να «εξηγήσουν τη βαρύτητα με κβαντομηχανικούς όρους», προκαλώντας την ανησυχία να βρούμε μια ενιαία θεωρία ενοποίησης για το σύμπαν. Δεν υπάρχει ακόμη τύχη, αλλά πολλοί πιστεύουν ότι υπάρχει.

«Υπάρχουν μερικές δύσκολες ερωτήσεις για την κβαντική βαρύτητα που δεν καταλαβαίνουμε ακόμα και χτυπάμε τα κεφάλια μας για πολύ καιρό», δήλωσε ο Sonner. «Πρέπει να βρούμε το σωστό δρόμο για την κατανόηση αυτών των ερωτήσεων.»
Η κβαντική εμπλοκή ακούγεται τόσο ξένη για την εμπειρία μας, επειδή φαίνεται να υπερβαίνει την ταχύτητα του φωτός, κάτι που παραβιάζει τη γενική σχετικότητα του Αϊνστάιν. (Το όριο ταχύτητας εξακολουθεί να δοκιμάζεται, φυσικά, γι 'αυτό και οι επιστήμονες ήταν τόσο ενθουσιασμένοι όταν φάνηκε ότι τα σωματίδια κινούνται γρηγορότερα από το φως σε ένα πείραμα του 2011 που αργότερα αποσυνδέθηκε λόγω ελαττωματικού αισθητήρα.)
Τέλος πάντων, έτσι προχώρησε η νέα έρευνα:
- Ο Sonner εξέτασε το έργο του Juan Maldacena του Ινστιτούτου Προηγμένων Μελετών και του Leonard Susskind του Πανεπιστημίου του Στάνφορντ. Οι φυσικοί έλεγαν πώς θα συμπεριφερόταν οι μπερδεμένες μαύρες τρύπες. «Όταν οι μαύρες τρύπες μπλέχτηκαν και μετά χωρίστηκαν, οι θεωρητικοί διαπίστωσαν ότι αυτό που προέκυψε ήταν μια σκουληκότρυπα - μια σήραγγα μέσω του χωροχρόνου που πιστεύεται ότι συγκρατείται από τη βαρύτητα. Η ιδέα φάνηκε να υποδηλώνει ότι, στην περίπτωση των σκουληκιών, η βαρύτητα προκύπτει από το πιο θεμελιώδες φαινόμενο των εμπλεγμένων μαύρων τρυπών », δήλωσε ο MIT.

- Ο Sonner έπειτα ξεκίνησε να δημιουργεί κουάρκ για να δει αν μπορούσε να παρακολουθήσει τι συμβαίνει όταν δύο είναι εμπλεγμένοι μεταξύ τους. Χρησιμοποιώντας ένα ηλεκτρικό πεδίο, μπόρεσε να πιάσει ζεύγη σωματιδίων που βγαίνουν από ένα περιβάλλον κενού με μερικά «παροδικά» σωματίδια σε αυτό.
- Μόλις έπιασε τα σωματίδια, τα χαρτογράφησε σε όρους χωροχρόνου (τετραδιάστατος χώρος). Σημείωση: η βαρύτητα πιστεύεται ότι είναι η πέμπτη διάσταση επειδή μπορεί να λυγίσει το χωροχρόνο, όπως μπορείτε να δείτε σε αυτές τις εικόνες γαλαξιών παρακάτω.
- Ο Sonner στη συνέχεια προσπάθησε να καταλάβει τι θα συνέβαινε στην πέμπτη διάσταση όταν τα κουάρκ μπλέκονταν στην τέταρτη διάσταση, χρησιμοποιώντας μια έννοια θεωρίας χορδών που ονομάζεται ολογραφική δυαδικότητα. «Ενώ ένα ολόγραμμα είναι ένα δισδιάστατο αντικείμενο, περιέχει όλες τις απαραίτητες πληροφορίες για την απεικόνιση τρισδιάστατης προβολής. Ουσιαστικά, η ολογραφική δυαδικότητα είναι ένας τρόπος για να αντλήσουμε μια πιο περίπλοκη διάσταση από την επόμενη χαμηλότερη διάσταση », δήλωσε ο MIT.

- Και κάτω από την ολογραφική δυαδικότητα, ο Sonner βρήκε μια σκουληκότρυπα. Η επίπτωση είναι αυτή η βαρύτηταεαυτόμπορεί να βγει από το μπλέξιμο αυτών των σωματιδίων, και ότι η κάμψη που βλέπουμε στο σύμπαν θα οφείλεται επίσης στην εμπλοκή.
«Είναι η πιο βασική αναπαράσταση που έχουμε εκεί όπου η εμπλοκή προκαλεί κάποιο είδος γεωμετρίας», δήλωσε ο Sonner. «Τι θα συμβεί αν χαθεί μέρος αυτής της εμπλοκής και τι συμβαίνει στη γεωμετρία; Υπάρχουν πολλοί δρόμοι που μπορούν να ακολουθηθούν και με αυτή την έννοια, αυτό το έργο μπορεί να αποδειχθεί πολύ χρήσιμο. "
Μπορείτε να δείτε την έρευνα στο Physical Review Letters.
Πηγή: Ινστιτούτο Τεχνολογίας της Μασαχουσέτης